- [Original Article]
- Sample on GitHub (WPF)
- Sample on Github (JavaScript)
- Live example in JavaScript (ReactJs)
Introduction
Interpolating points sometimes is hard mathematical work, even more, if the points are ordered. The solution is to create a function using the points and using an extra parameter t that represents the time dimension. This often is called a parametric representation of the curve. This article shows a simple way of interpolating a set of points using Bezier curves in WPF.
Background
The idea of this solution comes after asking this question in Stack Overflow. The accepted answer makes references to a simple and interesting method proposed by Maxim Shemanarev, where the control points are calculated from the original points (called anchor points).
Here, we create a WPF UserControl that draws the curve from any collection of points. This control can be used with the pattern MVVM. If any point's coordinate changes, the curve also will change automatically. For instance, it can be used for a draw application, where you can drag & drop the points for changing the drawing, or curve.
The Algorithm Behind
Due to the original antigrain site being down (I can find that Sourceforge is still supporting this library and we can find the original article over here!), I'm going to explain what is the algorithm proposed by Maxim Shemanarev.
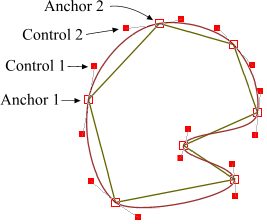
A Bezier curve has two anchor points (begin and end) and two control ones (CP) that determine its shape. Our anchor points are given, they are pair of vertices of the polygon. The question is, how to calculate the control points? It is obvious that the control points of two adjacent edges form one straight line along with the vertex between them.
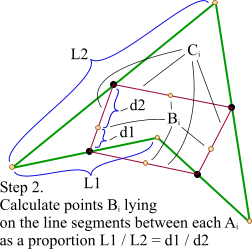
The solution found is a very simple method that does not require any complicated math. First, we take the polygon and calculate the middle points Ai of its edges.

Here, we have line segments Ci that connect two points Ai of the adjacent segments. Then, we should calculate points Bi as shown in this picture.
The third step is final. We simply move the line segments Ci in such a way that their points Bi coincide with the respective vertices. That's it, we calculated the control points for our Bezier curve and the result looks good.
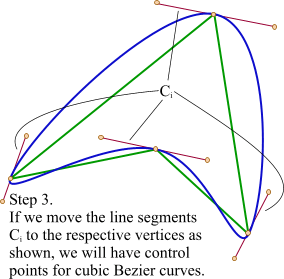
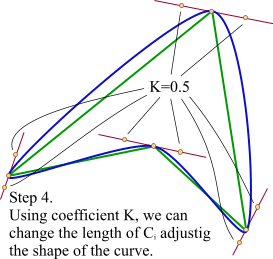
One little improvement. Since we have a straight line that determines the place of our control points, we can move them as we want, changing the shape of the resulting curve. I used a simple coefficient K that moves the points along with the line relative to the initial distance between vertices and control points. The closer the control points to the vertices are, the sharper figure will be obtained.
The method works quite well with self-intersecting polygons. The examples below show that the result is pretty interesting.
The Class for Calculation
Below is the class that makes the calculation of the spline segments, based on the algorithm, exposed above. This class is named InterpolationUtils, it has a static method (named InterpolatePointWithBezierCurves) that returns a list of BezierCurveSegment, that will be the solution to our problem.
The class BezierCurveSegment has the four properties that define a spline segment: StartPoint, EndPoint, FirstControlPoint, and the SecondControlPoint.
As the above algorithm was originally implemented for closed curves, and it is desired that it can be applied for open curves too, a little change is needed. For this reason, the InterpolatePointWithBezierCurves method receives a second parameter, a boolean variable named isClosedCurve, which determines if the algorithm will return an open or closed curve. Since we take four points (x1 = the current point, x2 = the next point, but also are required two more points for creating the three edges. x0 = the current's previous point and x3 = the next's next point), the x0 and x3 points selection will be like this:
- If it is a closed curve if x1 is the first point, then x0 is going to be the latest point (in this implementation, it is the latest but one because the latest point is the same as the first one), and if x2 is the latest point, then x3 is going to be the first point (in a similar way, in this implementation, is going to be the second point).
- If it is an open curve, then x0 = x1 and x3 = x2 for the previous cases.
The User Control
The user control that we propose is very simple to use, and it works with the MVVM pattern.
The LandMarkControl has only two dependency properties, one for the points, and another for the color of the curve. The most important property is the Points attached property. It is of IEnumerable type, and it assumes that each item has an X and Y properties.
In case the collection of points implements the INotifyCollectionChanged interface, the control will register to the CollectionChanged event, and if each point implements the INotifyPropertyChanged interface, the control also will register to the PropertyChanged event. In this way, every time any point is added or removed, or any point's coordinates changed, the control will be refreshed.
This is the complete user control code behind:
And this is the XAML code:
Examples of Usage
Using the control for creating the data template for the LandMarkViewModel:
Now everywhere a LandMarkViewModel is displayed, this data template will show the item as a LandMarkControl. It needs to be rendered on a Canvas:
This is a final image example: